Structure Tensor Total Variation

Posted on Edited on In
Symbols count in article: 10k Reading time ≈ 29 mins.
结构张量全变分

Foreword

// 论文2015年发表于 SIAM Journal on Imaging Sciences, 四位作者均大牛。

Conceptual Understanding

  • 对偶空间: 理解
  • Tensor 张量: 通俗解释
    疑惑点：到底是阶数还是维数？
  • Structure Tensor 结构张量：
      结构张量用于角点检测、边缘检测和纹理分析。对一副灰度图像，当两个相邻的像素点无限接近时，微分dI可以表示为：
    \[ \mathrm{d} I=\frac{\partial I}{\partial x} \mathrm{~d} x+\frac{\partial I}{\partial y} \mathrm{~d} y \]
      其平方范数可以表示为：
    \[ \|\mathrm{d} I\|^{2}=\sum_{m=x, y} \sum_{n=x, y}\left(\frac{\partial I}{\partial m} \cdot \frac{\partial I}{\partial n}\right) \mathrm{d} m \mathrm{~d} n=\left[\begin{array}{ll} \mathrm{d} x & \mathrm{~d} y \end{array}\right] T\left[\begin{array}{l} \mathrm{d} x \\ \mathrm{d} y \end{array}\right] \]

$$

$$

  其中，T是结构张量：
\[ T=\left[\begin{array}{cc} I_{x}^{2} & I_{x} I_{y} \\ I_{x} I_{y} & I_{y}^{2} \end{array}\right] \]
  其中\(I_{x}\)和\(I_{y}\)分别是沿x轴和y轴的一阶偏导数。矩阵T的行列式为K，迹为H。
  结构张量T为半正定矩阵，具有两个非负特征值，可以通过特征值将图像的空间结构信息分为三种：
  平坦区域：两个特征值\(\mu_{1}=\mu_{2}=0\)(H=0)，表示图像在该点任何方向灰度变化都很小；
  边缘区域：两个特征值\(\mu_{1}=\mu_{2}=0\)(H>0 & K=0)，表示图像在该点沿某一方向灰度变化率较大；
  角点区域：两个特征值\(\mu_{1}=\mu_{2}=0\)(H>0 & K>0)，表示图像在该点两个垂直方向上的灰度变化都很大；

Abstract

  • 引入一个新的一般能量泛函，用它来解决变分框架内的逆成像问题。
  • 所提出的正则化族称为结构张量全变分(STV)，它对结构张量的特征值进行惩罚，适用于灰度图像和向量值图像。
  • 推广了已有的几种变分惩罚，包括全变分半群及其向量扩展。同时，由于结构张量能够捕获局部邻域的一阶信息，STV泛函能够提供更稳健的图像变化度量。
  • 进一步证明了STV正则化是凸的，同时它们也满足图像变换的几个不变性。这些特性使它们成为成像应用的理想候选者。
  • 对于离散版本的STV泛函，推导了一个等价的定义，该定义基于补丁的雅可比算子，这是一种新的线性算子，扩展了雅可比矩阵。
  • 提出了关于各种逆成像问题的大量实验，将提出的正则化方法与其他正则化方法进行了比较。

Introduction

  • 逆问题越来越多地出现在一系列成像应用中。它们也出现在大量的计算机视觉应用中，包括运动估计、图像配准、立体声和密集三维(3D)重建。
  • 为了恢复的信息在物理上或统计上有意义，需要一个包含底层图像的已知属性的模型。
  • 处理不适定反问题的一种常用策略是变分法。这个框架的主要元素是正规化函数。
  • 最流行的成像应用正则化是全变分(TV)半范数。TV是一个凸函数，其成功的主要原因是它能够重建清晰、保存完好的图像边缘。然而，它的缺点是过度平滑均匀区域和产生阶梯伪影。

Regularization for Inverse Problems

problem formulation and variational recovery

  对于许多成像应用，采集是通过线性过程很好地描述的，可以用数学公式表示为: \[ \boldsymbol{v}(\boldsymbol{x}) \sim \mathcal{N}(\mathcal{A} \boldsymbol{u}(\boldsymbol{x})) \]   其中，\(\boldsymbol{u}(\boldsymbol{x})=\left[u_{1}(\boldsymbol{x}) \ldots u_{M}(\boldsymbol{x})\right]: \mathbb{R}^{2} \mapsto \mathbb{R}^{M}\)表示我们希望重建的具有M个通道的向量值的一般图像，A是一个线性算子，提供了从底层图像空间到测量空间的映射。符号N表示测量噪声，它包含了采集过程中所有可能的误差类型，包括随机噪声。
  从测量值v中恢复u属于线性逆问题的范畴。在大多数实际情况下，运算符A要么是病态的，要么是单数的。这种不适定性是在变分框架内处理的，其中u的重构是一个形式的目标函数的最小化问题: \[ \mathcal{E}(\boldsymbol{u})=\varphi(\mathcal{A} \boldsymbol{u})+\tau \psi(\boldsymbol{u}) \]   这个代价函数包括数据保真度项ϕ(Au)，它测量候选解对观测数据的解释程度，以及正则化ψ(u)，它编码关于底层图像的任何可用的先验信息。数据保真度项的确切形式取决于干扰测量的假定噪声模型。从贝叶斯的观点来看，整个重建方法对应于一个惩罚最大似然或最大后验估计问题。

TV regularization

  TV适用于灰度图像u(M = 1)，对于平滑图像定义为: \[ \operatorname{TV}(u)=\int_{\mathbb{R}^{2}}\|\nabla u\|_{2} \mathrm{~d} \boldsymbol{x} \]   TV的一个众所周知的缺点是，它支持分段常数解，它可以在图像的平滑区域创建强大的阶梯伪影。此外，TV和VTV的一个基本缺点是，用于惩罚图像在每个x点上变化的梯度大小作为图像描述符过于简单;它只依赖于x而不考虑其邻域的可用信息。

directional derivatives and the structure tensor

  目标是开发邻域感知的矢量图像变化的措施。
  假设向量值图像u属于Sobolev空间\(W^{1,2}\left(\mathbb{R}^{2}, \mathbb{R}^{M}\right)\)。设n为任意二维方向(\(\|\boldsymbol{n}\|_{2}=1\))。向量值图像u在n方向上以及任意特定图像点x处的矢量方向导数为： \[ \frac{\partial \boldsymbol{u}}{\partial \boldsymbol{n}}(\boldsymbol{x})=(J \boldsymbol{u}(\boldsymbol{x})) \boldsymbol{n} \]   u的Jacobian矩阵\(J \boldsymbol{u}\)定义为： \[ J \boldsymbol{u}(\boldsymbol{x})=\left[\nabla u_{1}(\boldsymbol{x}) \quad \ldots \quad \nabla u_{M}(\boldsymbol{x})\right]^{T} \]   方向导数\(\|\partial \boldsymbol{u} / \partial \boldsymbol{n}\|_{2}\)的大小衡量在n方向上任何一点x的图像变化量。这种方法的计算完全集中在x处。为了提高程序的鲁棒性和捕捉图像领域表现，用\(\|\partial \boldsymbol{u} / \partial \boldsymbol{n}\|_{2}\)的加权均方根代替，称之为方向变化： \[ \operatorname{RMS}_{K}\left\{\|\partial \boldsymbol{u} / \partial \boldsymbol{n}\|_{2}\right\}=\sqrt{K *\|\partial \boldsymbol{u} / \partial \boldsymbol{n}\|_{2}^{2}}=\sqrt{\boldsymbol{n}^{T}\left(S_{k} \boldsymbol{u}\right) \boldsymbol{n}} \]   在上面的方程中∗表示卷积运算，K(x)是一个非负的、旋转对称的卷积核，K(x) = K(|x|)，执行加权平均(例如，二维高斯分布)，\(S_{K} \boldsymbol{u}\)是图像u在x点处的结构张量，定义为： \[ S_{K} \boldsymbol{u}(\boldsymbol{x})=K *\left[J \boldsymbol{u}^{T} J \boldsymbol{u}\right](\boldsymbol{x}) \]

  设\(\lambda^{+}=\lambda^{+}\left(S_{K} \boldsymbol{u}(\boldsymbol{x})\right), \lambda^{-}=\lambda^{-}\left(S_{K} \boldsymbol{u}(\boldsymbol{x})\right)\)是\(S_{K} \boldsymbol{u}(\boldsymbol{x})\)的特征值，\(\lambda^{+} \geq \lambda^{-}\)， \(\boldsymbol{\theta}^{+}, \boldsymbol{\theta}^{-}\)是对应的特征向量。\(\omega \in(-\pi, \pi]\)定义为方向向量n与特征向量\({\theta}^{+}\)之间的夹角。利用特征分解，方向变化可以被定义为角度\(\omega\)的函数： \[ V(\omega) \triangleq \operatorname{RMS}_{K}\left\{\|\partial \boldsymbol{u} / \partial \boldsymbol{n}\|_{2}\right\}=\sqrt{\lambda^{+} \cos ^{2} \omega+\lambda^{-} \sin ^{2} \omega} \]

  由上述参数得到椭圆： \[ \boldsymbol{P}(\omega)=\cos \omega \sqrt{\lambda^{+}} \boldsymbol{\theta}^{+}+\sin \omega \sqrt{\lambda^{-}} \boldsymbol{\theta}^{-}, \omega \in[0,2 \pi) \]

结构张量椭圆可视化结果

  椭圆的长半径和小半径分别为\(\sqrt{\lambda^{+}}\)和\(\sqrt{\lambda^{-}}\)，而长轴的方向分别为\({\theta}^{+}\)和\({\theta}^{-}\)。其特征向量 \({\theta}^{+}\)和\({\theta}^{-}\)描述了u的最大和最小矢量变化的方向, 特征值平方根\(\sqrt{\lambda^{+}}\)和\(\sqrt{\lambda^{-}}\) 描述了这些变化的大小。 更重要的是，观察到\(V(\omega)=\|\boldsymbol{P}(\omega)\|_{2}\)，意味着方向变化V(ω)可以解释为任意点P(ω)到椭圆中心的距离。

the structure tensor TV functional

  为了设计一个正则化器来整合每个图像点的局部图像变化的标量惩罚，我们需要考虑提供函数V (ω)的度量。这些测度也是从结构张量的特征值计算出来的，分以下几种:
  Case 1. RMS of \(V(\omega):\left((2 \pi)^{-1} \int_{0}^{2 \pi} V^{2}(\omega) \mathrm{d} \omega\right)^{1 / 2}=\sqrt{\lambda^{+}+\lambda^{-}} / \sqrt{2}\)
  Case 2. Maximum of \(V(\omega):\sqrt{\lambda^{+}}\)
  Case 3. Midrange of \(V(\omega):\sqrt{\lambda^{+}+\lambda^{-}} / 2\)
  对于每个图像点x，定义二维向量:
\[ \sqrt{\boldsymbol{\lambda}}=\sqrt{\boldsymbol{\lambda}\left(S_{K} \boldsymbol{u}(\boldsymbol{x})\right)}=\left(\sqrt{\lambda^{+}\left(S_{K} \boldsymbol{u}(\boldsymbol{x})\right)}, \sqrt{\lambda^{-}\left(S_{K} \boldsymbol{u}(\boldsymbol{x})\right)}\right) \]

  上面三种情况对应的范数：\(\|\sqrt{\boldsymbol{\lambda}}\|_{2}(\) Case 1\(),\|\sqrt{\boldsymbol{\lambda}}\|_{\infty}(\) Case 2\(),\|\sqrt{\boldsymbol{\lambda}}\|_{1}(\) Case 3\()\)。进一步考虑大于等于1的P范数作为图像变化的度量。这些标准测量图像变化比在TV中使用的梯度幅度更连贯和稳健，因为它们考虑到其附近的变化。同时，由于它们同时依赖于方向变化的最大值和最小值，因此它们包含了更丰富的信息。通过这种方式，它们的响应通常更好地适应图像的几何形状。

  定义以下全新正则项：
\[ \mathrm{STV}_{p}(\boldsymbol{u})=\int_{\mathbb{R}^{2}}\left\|\left(\sqrt{\lambda^{+}}, \sqrt{\lambda^{-}}\right)\right\|_{p} \mathrm{~d} \boldsymbol{x} \]   以上结构张量正则化项是平移和旋转不变的、1阶齐次、凸的。

Discrete STV

  需要处理离散数据
### notation and definitions   对图像使用镜像边界拓展。离散STV形式： \[ \operatorname{STV}_{p}(\boldsymbol{u})=\sum_{n=1}^{N}\left\|\left(\sqrt{\lambda_{n}^{+}}, \sqrt{\lambda_{n}^{-}}\right)\right\|_{p} \]

patch-based Jacobian operator

  正则化依赖于结构张量的特征值。但是算子的非线性和卷积核的存在,使泛函的最小化变得困难。
  为解决以上问题，提出基于局部加权面片的图像雅可比算子。这种新的算子，称之为patch-based Jacobian，包含了由平滑核确定的加权移位版本的雅可比。
  patch-based Jacobian 定义： \[ \boldsymbol{J}_{K}: \mathbb{R}^{N M} \mapsto \mathcal{X} \]   其中，\(\mathcal{X} \triangleq \mathbb{R}^{N \times(L M) \times 2}\) and \(L=\left(2 L_{K}+1\right)^{2}\)

  这个定义意味着，如果我们在u的第n个像素上应用patch-based Jacobian，那么结果是一个大小为LM*2的矩阵，用\(\left[\boldsymbol{J}_{K} \boldsymbol{u}\right]_{n}\)表示。 \[ \left[\boldsymbol{J}_{K} \boldsymbol{u}\right]_{n}=\left(\left[\tilde{\nabla} \boldsymbol{u}_{1}\right]_{n}, \ldots,\left[\tilde{\nabla} \boldsymbol{u}_{M}\right]_{n}\right)^{T} \]   其中， \[ \left[\tilde{\nabla} \boldsymbol{u}_{m}\right]_{n}=\left(\left[T_{s_{1}, \omega} \circ \nabla \boldsymbol{u}_{m}\right]_{n}, \ldots,\left[T_{s_{L}, \omega} \circ \nabla \boldsymbol{u}_{m}\right]_{n}\right) \]   \(\nabla\)是离散梯度，\((\cdot)^{T}\)是转置算子，\(\circ\)表示算子的组成，移位向量\(\boldsymbol{s}_{l}(l=1, \ldots, L)\)是晶格\(\mathcal{P}\)的元素，\(T_{s_{1}, \omega}\)是加权平移算子，后者考虑了镜像边界条件，定义为： \[ \left[T_{s_{l}, \omega} \circ \nabla \boldsymbol{u}_{m}\right]_{n}=\boldsymbol{\omega}\left[\boldsymbol{s}_{l}\right] \nabla \boldsymbol{u}_{m}\left[\boldsymbol{x}_{n}-\boldsymbol{s}_{l}\right] \]

  定义空间\(\mathcal{X}\)的内积： \[ \langle\boldsymbol{X}, \boldsymbol{Y}\rangle_{\mathcal{X}}=\sum_{n=1}^{N} \operatorname{trace}\left(\boldsymbol{Y}_{n}^{T} \boldsymbol{X}_{n}\right) \]   定义空间\(\mathcal{X}\)的范数： \[ \|\boldsymbol{X}\|_{\mathcal{X}}=\sqrt{\langle\boldsymbol{X}, \boldsymbol{X}\rangle_{\mathcal{X}}}=\left(\sum_{n=1}^{N}\left\|\boldsymbol{X}_{n}\right\|_{F}^{2}\right)^{\frac{1}{2}} \]

equivalent formulation of the discrete STV

  在像素位置n处评估的u的离散结构张量可以根据patch-based Jacobian写成: \[ \left[\boldsymbol{S}_{K} \boldsymbol{u}\right]_{n}=\left[\boldsymbol{J}_{K} \boldsymbol{u}\right]_{n}^{T}\left[\boldsymbol{J}_{K} \boldsymbol{u}\right]_{n} \]

Discrete STV Minimization

proximal map of \(\mathrm{STV}_{p}\)

  函数ψ的最近邻映射或Moreau邻近算子表示为: \[ \operatorname{prox}_{\psi}(\mathbf{z})=\underset{\boldsymbol{u}}{\arg \min } \frac{1}{2}\|\boldsymbol{u}-\mathbf{z}\|_{2}^{2}+\psi(\boldsymbol{u}) \]   在本文中，\(\psi(\boldsymbol{u})=\tau \mathrm{STV}_{p}(\boldsymbol{u})+\iota_{\mathcal{C}}\)

有： \[ \underset{\boldsymbol{u}}{\arg \min } \frac{1}{2}\|\boldsymbol{u}-\mathbf{z}\|_{2}^{2}+\tau \operatorname{STV}_{p}(\boldsymbol{u})+\iota_{\mathcal{C}}(\boldsymbol{u}) \]

solving the dual problem

  作为约束优化问题的解:

\[ \hat{\boldsymbol{\Omega}}=\underset{\boldsymbol{\Omega} \in \mathcal{B}_{\infty, q}}{\arg \max } \frac{1}{2}\left\|\boldsymbol{w}-\Pi_{C}(\boldsymbol{w})\right\|_{2}^{2}+\frac{1}{2}\left(\|\boldsymbol{z}\|_{2}^{2}-\|\boldsymbol{w}\|_{2}^{2}\right) \]

  梯度

\[ \nabla d(\mathbf{\Omega})=\tau \boldsymbol{J}_{K} \Pi_{C}\left(\mathbf{z}-\tau \boldsymbol{J}_{K}^{*} \boldsymbol{\Omega}\right) \]

numerical algorithm

  调用一个基于梯度的方案来导出对偶问题的解。在这项工作中，对光滑函数采用内斯特罗夫迭代法。该方案显示出比标准梯度上升法高一个数量级的收敛速度。由于我们的双目标是光滑的，具有李普希茨连续梯度，使用了一个常数步长，等Lipschitz常数的倒数。 \[ L(d) \leq 8 \sqrt{2} \tau^{2} \]

solution of general inverse problems

  这个基本工具也可以用来解决更一般的反问题。

Application and Experiments

experimental setting

  • 为验证所提出的STV正则化方法的有效性，我们在几个逆成像问题上将它们与其他相关方法进行了比较。特别考虑了图像恢复(去噪和去模糊)、图像放大和从有限数量的傅立叶测量进行图像重建的问题。

  • 在所有情况下，图像强度被归一化，使得它们位于范围[0，1]内。

  • 比较项：考虑TGV的二阶扩展 \[ \operatorname{TGV}_{\alpha}^{2}(\boldsymbol{u})=\min _{\boldsymbol{v} \in \mathbb{R}^{N \times 2}}\|\nabla \boldsymbol{u}-\boldsymbol{v}\|_{2}+\alpha\|\mathcal{E} \boldsymbol{v}\|_{F} \]

  • 算子\(\mathcal{E}\)表示对称梯度，\(\mathcal{E} \boldsymbol{v}=0.5\left(\nabla \boldsymbol{v}+\nabla \boldsymbol{v}^{T}\right)\) ,\(\alpha\)是用于平衡一阶项和二阶项的权重值，在这里取2。

  • 对于结构张量定义中的卷积核K，定义其为标准差\(\sigma=0.5\)高斯分布的像素块，窗口大小3*3。

  • 四种噪声水平下不同正则化方法的图像去噪比较。性能是以相对于噪声输入的平均信噪比改善(分贝)来衡量的。

image restoration

  • 对于图像去噪问题，考虑独立同分布高斯噪声和分别对应于标准偏差\(\sigma_{w}=\{0.1,0.15,0.2,0.25\}\)的四种不同噪声水平。
  • 在灰度实验中，TV是所有噪声水平中表现最差的方法。TGV比TV有所改进，这反映了它更倾向于分段线性而不是分段常数解，从而避免了TV的阶梯伪影。我们两个版本的正则化器，STV1和STV1，系统地优于TV和TGV2。

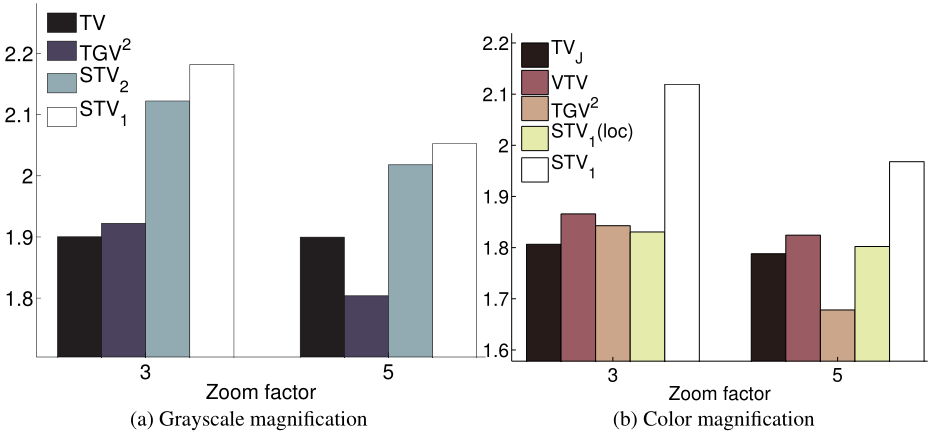
image magnification

  图像放大是一个与图像去模糊密切相关的反问题。 再次验证了STV 1不仅提高了信噪比，还导致了增强视觉质量的重建。

三个峰值信噪比和四个噪声水平下不同正则化方法的图像去模糊比较。性能是以相对于降级输入的平均PSNR改善(单位为分贝)来衡量的。最上面一行的条形代表灰度结果，而最下面一行的条形代表彩色结果
图像去模糊示例:输入和最佳结果的特写
两种变焦因子下不同正则化因子的图像放大比较
图像放大示例:输入和最佳结果的特写镜头。输入通过简单的零阶保持放大。顶行:缩放因子d = 5时输入的灰度放大倍数。底行:缩放因子d = 5的输入的颜色放大倍数

reconstruction from sparse Fourier measurements

  考虑从有限数量的傅立叶测量中重建图像的问题。

implementation details and computational runtimes

  由于卷积核的存在，所提出的Stv2和Stv1函数在当前实现中大约慢3.5-4倍。

Conclusions

  • 引入了一个新的凸能量泛函族，它扩展和推广了全变分半范数及其向量扩展。
  • 我们的泛函的关键特征是，它们通过惩罚结构张量在这一点上的特征值，结合了图像域中每个点附近的信息。因此，它们提供了更丰富、更稳健的图像变化度量，从而提高了重建性能。
  • 在几个逆成像问题上与竞争方法进行了比较,验证提出的正则化可以代替TV或其矢量扩展。